->

ABSTRAIT

Nous proposons un nouveau type de réseaux neuronaux pour le contrôle structurel, qui comprend un espace d’entrée adaptatif. Cette fonction est spécialement conçue pour la sélection d’entrée séquentielle lors de l’identification adaptative et du contrôle de non-linéaires systèmes, ce qui permet à l’espace d’entrée d’être organisé de manière dynamique, pendant que l’excitation se produit. Le réseau de neurones présente les principaux avantages de (1) automatiser le processus de sélection des entrées pour des séries temporelles non connues a priori; (2) adapter la représentation aux non-stationnaires; et (3) en utilisant des observations limitées.

L’algorithme conçu pour l’espace d’entrée adaptatif suppose une quasi-stationnarité locale de la série temporelle et intègre des cartes locales séquentiellement dans un vecteur de retard en utilisant le théorème d’incorporation. L’espace d’entrée de la représentation, qui dans notre cas est un réseau de neurones en ondelettes, est ensuite mis à jour. Nous démontrons que le réseau de neurones a le potentiel d’améliorer considérablement la convergence d’un modèle de boîte noire dans le suivi adaptatif d’un système non linéaire. Ses performances sont ensuite évaluées dans une simulation grandeur nature d’une structure civile existante soumise à des excitations non stationnaires (vent et tremblements de terre) et montre la supériorité de la méthode proposée.

ARCHITECTURE DU CONTRÔLEUR

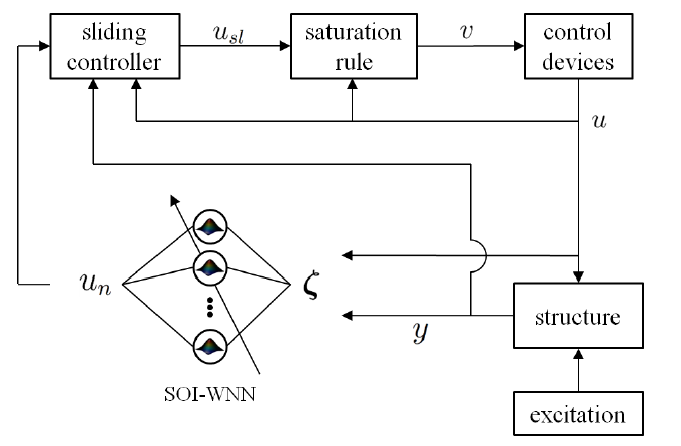
Figure 1: Schéma fonctionnel du système de contrôle en boucle fermée.

La figure 1 montre une représentation du contrôleur pour des applications spécifiques au contrôle structurel semi-actif. La structure est soumise à un forçage externe (excitation) et à des efforts des dispositifs de commande. Les états dynamiques y et les forces de contrôle u sont alimentés dans le SOI-WNN adaptatif sous le vecteur d’entrée ζ pour obtenir la force de contrôle neuro u_n. Un contrôleur coulissant modifie u_n pour tenir compte de la grande région de force inaccessible résultant du dispositif semi-actif, et la force résultante u_sl est utilisé pour déterminer la tension v dans le dispositif de commande, qui régit la force de commande finale u.

FONCTION D’AUTO-ORGANISATION

Figure 3: Illustration du théorème d’intégration de Takens.

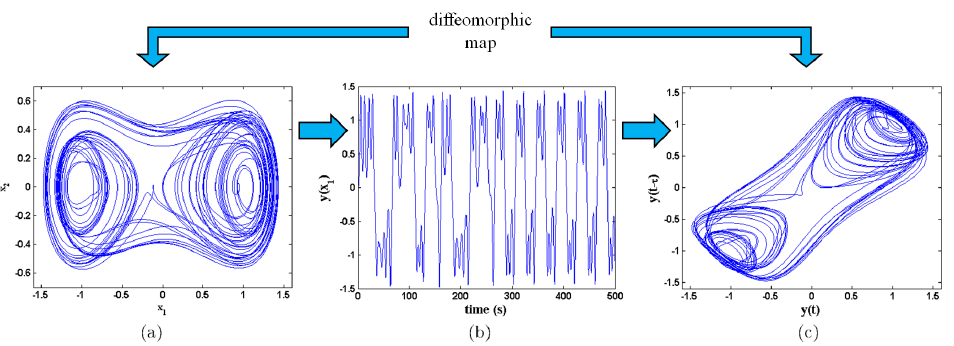
Figure 3: Illustration du théorème d’intégration de Takens. a) Espace de phase du système inconnu à reconstruire (ici une représentation bidimensionnelle d’un système Du-ffing y = h (x₁; X₂; X₃); b) les mesures de séries chronologiques y sont prises à partir d’un seul état (y (x₁) = x₁ du système inconnu; et c) l’espace de phase du système inconnu peut être reconstruit de manière difféomorphique, ici dans un espace de phase à 2 dimensions construit à partir de y avec un retard temporel T.

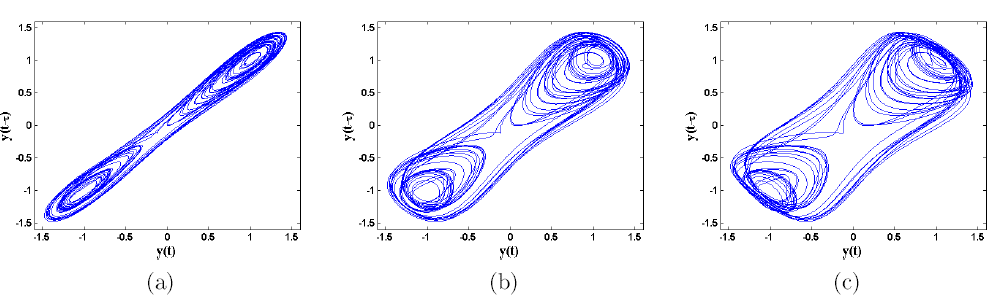
Figure 4: Dépliage de l’espace d’états en fonction de T. a) T = 0: 5 s; b) T = 1: 4 s; et c) T = 2 s.

L’objectif du test MI est de trouver une temporisation appropriée T pour représenter la dynamique essentielle d’un système. Prenez le système bidimensionnel de la figure 3 par exemple. Si l’on essaie de reconstruire l’espace des phases en utilisant y (k) et y (kT ), une petite valeur pour T réduira l’espace de phase à une ligne de 45 degrés. Qualitativement, T doit être augmenté pour déployer l’espace des phases jusqu’à ce que suffisamment d’informations de la dynamique puissent être extraites. Si T est trop élevé, l’espace de phase se serait trop déplié et les informations seront perdues. La figure 4 illustre le principe du système inconnu représenté sur la figure 3.

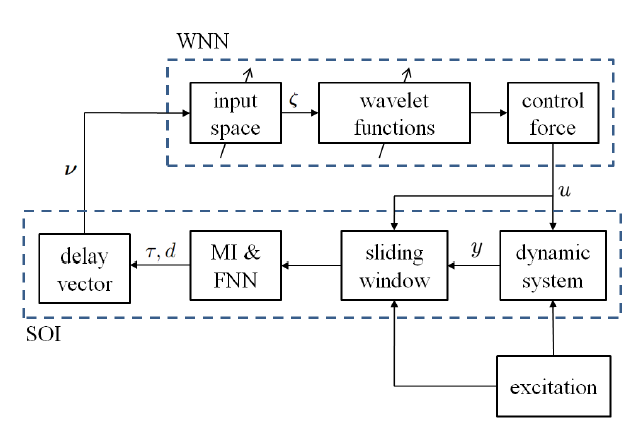
Figure 5: Schéma fonctionnel du SOI-WNN proposé.

La figure 5 résume l’algorithme SOI intégré au WNN, qui est le SOI-WNN proposé. Dans la figure, l’algorithme SOI sélectionne les valeurs de T et d en utilisant les méthodes MI et FNN sur le dernier état n et des observations d’entrée à partir de la fenêtre glissante. Dans le cas où l’excitation n’est pas observable, le vecteur de retard peut être construit en surintégrant l’observation d’état y. Un vecteur de retard est construit et devient l’espace d’entrée objectif. L’espace d’entrée réel ζ du WNN est adapté en douceur en fonction de, et un nouveau forçage u est calculé.

FONCTION D’AUTO-ADAPTATION

Les paramètres SOI-WNN sont continuellement adaptés vers l’optimalité. Compte tenu de l’excitation non stationnaire et de l’intégration de dispositifs semi-actifs dans le système en boucle fermée, la règle de commande adaptative ne devrait pas converger. Cette section dérive les règles d’adaptation des paramètres. Pour plus de clarté, la dérivation est spécialisée pour une sortie de force scalaire (un seul dispositif de contrôle). Les règles d’adaptation peuvent être facilement étendues à plusieurs dispositifs de contrôle en utilisant la notation matricielle. Néanmoins, il peut être utile dans les applications de considérer des contrôleurs décentralisés, pour lesquels la notation scalaire s’applique.

SÉLECTION DES PARAMÈTRES

La sélection des paramètres est une tâche fondamentale dans la conception de réseaux de neurones. Dans le contrôle structurel, il n’est pas rare que les paramètres non adaptatifs soient réglés jusqu’à ce que la satisfaction de la performance soit atteinte. Pour rester cohérent avec l’application proposée du contrôleur, on ne peut pas se fier à cette opportunité de réglage des paramètres. Le but de cette section est de fournir une discussion sur le choix des paramètres pour le réseau neuronal, dans le but de donner des conseils dans la conception du contrôleur basé sur une connaissance limitée d’une structure.

EXEMPLE SYNTHÉTIQUE

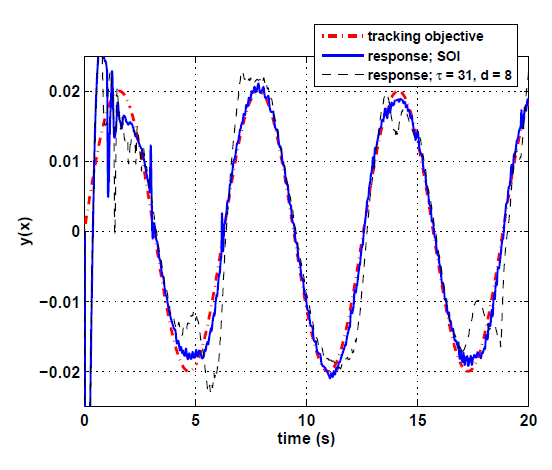
Figure 6: Réponses de séries chronologiques. Le SOI-WNN (ligne droite bleue) converge plus rapidement que le WNN à entrée fixe optimal (ligne pointillée noire).

La figure 6 montre la réponse en série chronologique de l’algorithme SOI par rapport aux paramètres fixes optimaux. L’algorithme SOI (ligne droite bleue) permet une convergence plus rapide et de meilleurs résultats de suivi que le WNN à entrée fixe optimal (ligne pointillée noire). Cela est dû à la dynamique de la règle de contrôle changeant avec le temps, pour laquelle l’adaptation de l’espace d’entrée se traduit par une représentation plus efficace, comme supposé. Le tableau 2 montre l’erreur RMS pour les quatre stratégies d’entrée sur un temps de suivi de 20 s, ainsi que la taille moyenne du réseau (nombre de nœuds masqués).

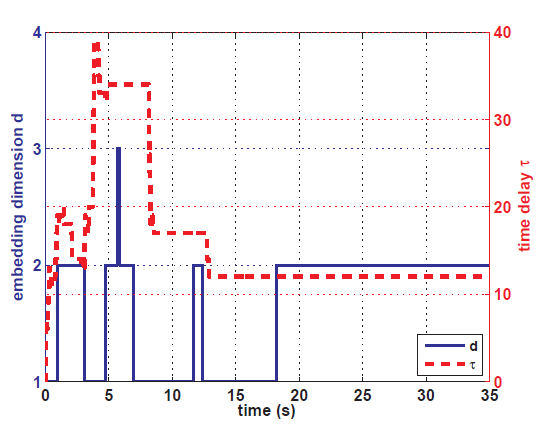
Figure 9: Identification de T et d fixes pour une représentation globale.

Afin d’identifier les entrées fixes (statiques) pour la représentation, l’algorithme SOI est désactivé une fois que la métrique d’erreur reste en dessous d’un seuil pour un nombre prédéfini d’étapes. Pour cette tâche, la capacité du réseau à élaguer les nœuds a été assouplie, car nous prévoyons avoir besoin d’un réseau plus dense pour construire une représentation précise de la dynamique globale. La figure 9 montre l’évolution des paramètres d’entrée au fil du temps, illustrant la nature auto-organisée de l’espace d’entrée.

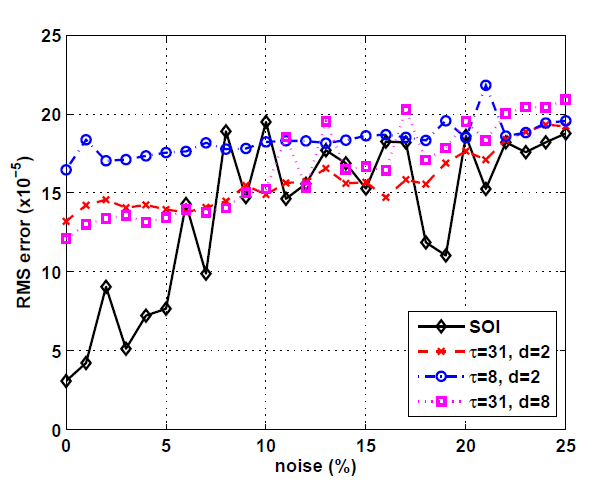
Figure 10: Erreur RMS par rapport au bruit, après 5 s (x10-5).

Ici, différents niveaux de bruit gaussien ont été induits dans les observations pour étudier les performances sous bruit. La figure 10 montre l’erreur RMS pour un bruit compris entre 0% et 25%. Le SOI-WNN est capable de surpasser considérablement toutes les stratégies optimales à entrée fixe pour un bruit inférieur à 5%. Cependant, au-dessus de ce niveau, la performance relative de l’algorithme diminue rapidement, avec une tendance à fonctionner de la même manière que les stratégies à entrées fixes.

SIMULATION PLEINE ÉCHELLE

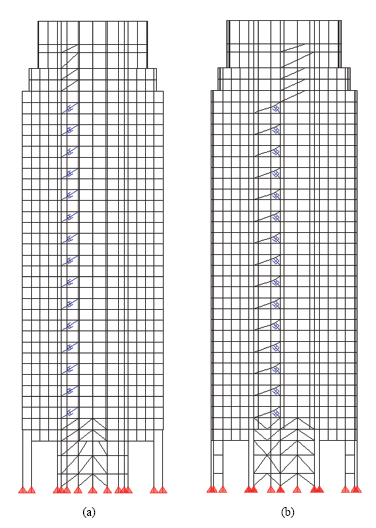
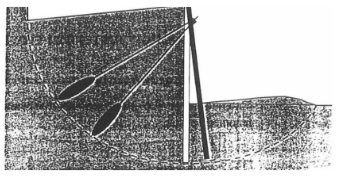
Figure 11: Vue en élévation de la structure simulée: a) direction X; et b) direction Y.

La structure simulée est une tour de bureaux de 39 étages située dans le centre-ville de Boston, Massachussets. Il a été construit en 1990 avec un système d’amortissement visqueux pour atténuer les vibrations excessives du vent causées par une tour à proximité. La stratégie de conception et l’évaluation des performances du système d’amortissement visqueux sont documentées. La tour comprend deux amortisseurs visqueux dans chaque direction (direction X et Y) un étage sur deux, entre les étages 5 et 33, pour un total de 60 amortisseurs visqueux. La figure 11 montre une vue en élévation de la structure dans les deux directions avec l’emplacement des amortisseurs.

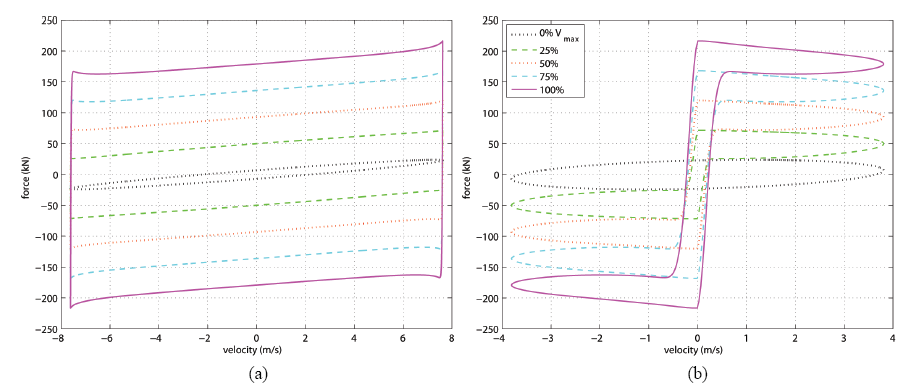
Figure 12: dynamique du MFD sous une excitation sinusoïdale d’amplitude de 7,62 mm de 0,5 Hz: a) déplacement de force; et b) force-vitesse.

Dans les simulations, les amortisseurs visqueux sont remplacés par des amortisseurs à friction variable de capacité similaire, appelés dispositifs à friction modifiée (MFD). Le dispositif semi-actif consiste en un mécanisme de frein à tambour installé en parallèle avec un élément visqueux et un élément étouffant. Le frein à tambour est équipé d’un actionneur linéaire, dont la force est sensiblement amplifiée par le mécanisme d’auto-excitation du frein. L’appareil peut théoriquement produire une plage de force d’amortissement de 0 à 1350 en utilisant quelques actionneurs linéaires fonctionnant sur batteries. Le MFD a été conçu pour imiter la dynamique d’un amortisseur MR. La figure 12 présente la dynamique idéalisée d’un MFD de 200 kN sur divers niveaux de tension.

DISCUSSION ET CONCLUSION

Un nouveau neurocontrôleur a été présenté pour le contrôle semi-actif des structures civiles. Le contrôleur est un réseau neuronal à ondelettes adaptatif, pour lequel la nouvelle fonctionnalité est un espace d’entrée auto-adaptatif utilisant l’algorithme SOI. Le SOI-WNN peut mettre à jour séquentiellement son espace d’entrée sur la base de mesures limitées et locales, pendant qu’une excitation se produit, ce qui conduit à une représentation plus efficace en raison des non-stations du système.

L’exemple synthétique de la section 6 a démontré que l’algorithme SOI était une fonctionnalité puissante. Pour l’exemple, l’algorithme SOI s’est avéré la meilleure option d’entrée pour obtenir un taux de convergence rapide par rapport aux stratégies d’entrée fixes optimisées. Cette haute performance a été atteinte avec un bon niveau de stabilité et un temps de calcul acceptable par rapport à la taille de la fenêtre glissante, et le SOI-WNN était nettement meilleur que toutes les stratégies à entrée fixe sur l’espace de recherche fourni pour les niveaux de bruit entre 0-5% . Sur la base des excellentes performances de l’exemple synthétique de faible dimension, le SOI-WNN a été simulé sur une structure grandeur nature équipée de dispositifs de contrôle semi-actifs (non linéaires), soumis à des excitations de vent et de tremblement de terre.

Les résultats de l’excitation du vent ont montré que le SOI-WNN était capable d’atteindre, au moins, le même niveau de performance que le contrôleur LQR, sinon mieux. Il a également surpassé toutes les stratégies à entrées fixes optimisées sur l’espace de recherche fourni, en utilisant moins d’énergie. De telles performances élevées sont similaires à l’exemple synthétique, et peuvent s’expliquer par la réponse de faible dimension de la structure lorsqu’elle est soumise à des excitations de vent, malgré leur nature non stationnaire.

Source: Université d’État de l’Iowa
Auteurs: Simon Laflamme | J. J.E. Slotine | J.J. Connor

Télécharger le projet