Programme C pour la méthode d’élimination de Gauss

En ingénierie et en science, la solution d’équations linéaires simultanées est très importante. Différentes analyses telles que des circuits électroniques comportant des éléments invariants, un réseau en condition stationnaire et sinusoïdale, la sortie d’une usine chimique et la recherche du coût des réactions chimiques dans de telles usines nécessitent la solution d’équations linéaires simultanées.
Dans la méthode de Gauss-Elimination, ces équations sont résolues en éliminant les inconnues successivement. le Programme C pour la méthode d’élimination de Gauss réduit le système à un matrice triangulaire supérieure à partir de laquelle les inconnues sont dérivées par l’utilisation de la méthode de substitution vers l’arrière.
Le pivotement, partiel ou complet, peut être effectué dans la méthode d’élimination de Gauss. Donc, cette méthode est quelque peu supérieure à la Méthode Gauss Jordan. Cette approche, combinée à la substitution arrière, est assez générale. Il est couramment utilisé et peut être bien adopté pour écrire un programme pour Méthode d’élimination de Gauss en C.
Pour cela, considérons d’abord les trois équations suivantes:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
En supposant que a1 ≠ 0, x est éliminé de la deuxième équation en soustrayant (a2 / a1) fois la première équation de la deuxième équation. De la même manière, le code C présenté ici élimine x de la troisième équation en soustrayant (a3 / a1) fois la première équation de la troisième équation.
Ensuite, nous obtenons les nouvelles équations comme:
a1x + b1y + c1z = d1
b’2y + c’2z = d’2
c’’3z = d’’3
La procédure d’élimination se poursuit jusqu’à ce qu’une seule inconnue reste dans la dernière équation. Une fois sa valeur déterminée, la procédure est arrêtée. Maintenant, Élimination de Gauss en C utilise la substitution inverse pour obtenir les valeurs de x, y et z comme:
z = d’’3 / c’’3
y = (d’2 – c’2z) / b’2
x = (d1- c1z- b1y) / a1
Code source de la méthode d’élimination de Gauss en C:
1 2 3 4 5 6 7 8 9 dix 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | #comprendre int principale() { int je,j,k,n; flotte UNE[[[[20][[[[20],c,X[[[[dix],somme=0,0; printf( » nSaisissez l’ordre de la matrice: »); scanf(« %ré »,&n); printf( » nSaisissez les éléments de la matrice augmentée par ligne: n n »); pour(je=1; je<=n; je++) { pour(j=1; j<=(n+1); j++) { printf(« UNE[%d][%d] : « , je,j); scanf(« %F »,&UNE[[[[je][[[[j]); } } pour(j=1; j<=n; j++) / * boucle pour la génération de la matrice triangulaire supérieure * / { pour(je=1; je<=n; je++) { si(je>j) { c=UNE[[[[je][[[[j]/UNE[[[[j][[[[j]; pour(k=1; k<=n+1; k++) { UNE[[[[je][[[[k]=UNE[[[[je][[[[k]–c*UNE[[[[j][[[[k]; } } } } X[[[[n]=UNE[[[[n][[[[n+1]/UNE[[[[n][[[[n]; / * cette boucle est pour la substitution vers l’arrière * / pour(je=n–1; je> =1; je–) { somme=0; pour(j=je+1; j<=n; j++) { somme=somme+UNE[[[[je][[[[j]*X[[[[j]; } X[[[[je]=(UNE[[[[je][[[[n+1]–somme)/UNE[[[[je][[[[je]; } printf( » nLa solution est: n »); pour(je=1; je<=n; je++) { printf( » nx% d =% f t »,je,X[[[[je]); / * x1, x2, x3 sont les solutions requises * / } revenir(0); } |
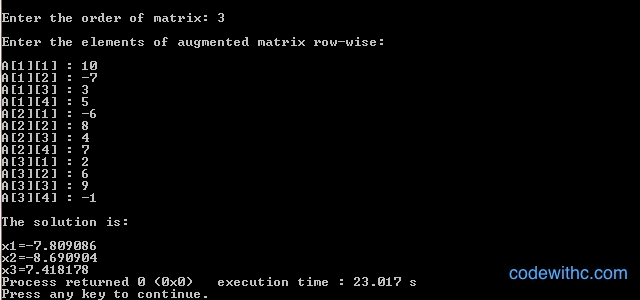
Entrée sortie:
Regarde aussi,
Programme MATLAB d’élimination de Gauss
Algorithme / organigramme d’élimination de Gauss
Compilation de didacticiels sur les méthodes numériques
Le code source de Gauss Elimination en C doit être compilé dans Code :: Blocks. Le programme est testé et ne contient aucun bug. Si vous avez des questions concernant la méthode d’élimination de Gauss ou son programme susmentionné, faites-les sortir de la zone de commentaires.