Programme C pour la méthode Regula Falsi

Méthode Regula Falsi, également connue sous le nom de méthode de la fausse position, est l’approche la plus ancienne pour trouver la racine réelle d’une fonction. Il s’agit d’une méthode de parenthèse fermée et ressemble étroitement à la méthode de bissection.
le Programme C pour la méthode regula falsi nécessite deux suppositions initiales de nature opposée. Comme le méthode sécante, l’interpolation est effectuée pour trouver les nouvelles valeurs pour les itérations successives, mais dans cette méthode, un intervalle reste toujours constant.
L’effort de programmation pour Regula Falsi ou méthode des fausses positions en C la langue est simple et facile. La convergence est de premier ordre et elle est garantie. Dans approche manuelle, la méthode de la fausse position peut être lente, mais elle se révèle supérieure à la méthode de la bissection.
Caractéristiques de la méthode Regula Falsi:
- Type – support fermé
- Nombre de suppositions initiales – 2
- Convergence – linéaire
- Taux de convergence – lent
- Précision – bonne
- Effort de programmation – facile
- Approche – interpolation
Vous trouverez ci-dessous un code source court et simple dans Programme C pour la méthode Regula Falsi pour trouver la racine de cos (x) – x * e ^ x. Ici, x0 et x1 sont les suppositions initiales prises.
Variables:
- itr – un compteur qui garde la trace du no. d’itérations effectuées
- maxmitr – nombre maximum d’itérations à effectuer
- x0, x1 – les limites dans lesquelles se trouve la racine
- x2 – la valeur de root à la nième itération
- x3 – la valeur de root à (n + 1) ème itération
- allerr – erreur autorisée
- x – valeur de root à la nième itération dans la fonction regula
- f (x0), f (x1) – les valeurs de f (x) à x0 et x1 respectivement
f (x) = cos (x) – x * e ^ x
Code source de la méthode Regula Falsi en C:
1 2 3 4 5 6 7 8 9 dix 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | #comprendre #comprendre flotte F(flotte X) { revenir cos(X) – X*exp(X); } néant regula (flotte *X, flotte x0, flotte x1, flotte fx0, flotte fx1, int *itr) { *X = x0 – ((x1 – x0) / (fx1 – fx0))*fx0; ++(*itr); printf(« N ° d’itération.% 3d X =% 7.5f n », *itr, *X); } néant principale () { int itr = 0, maxmitr; flotte x0,x1,x2,x3,allerr; printf( » nSaisissez les valeurs de x0, x1, des erreurs autorisées et des itérations maximales: n »); scanf(« % f% f% f% d », &x0, &x1, &allerr, &maxmitr); regula (&x2, x0, x1, F(x0), F(x1), &itr); faire { si (F(x0)*F(x2) < 0) x1=x2; autre x0=x2; regula (&x3, x0, x1, F(x0), F(x1), &itr); si (fabs(x3–x2) < allerr) { printf(« Après% d itérations, root =% 6.4f n », itr, x3); revenir 0; } x2=x3; } tandis que (itr<maxmitr); printf(« La solution ne converge pas ou les itérations ne suffisent pas: n »); revenir 1; } |
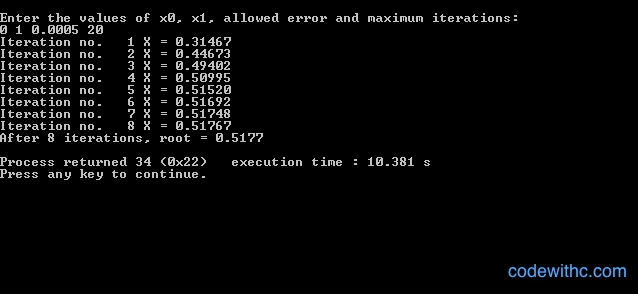
Entrée sortie:
Regarde aussi,
Méthode MATULAB de Regula Falsi
Algorithme / organigramme de la méthode Regula Falsi
Compilation de didacticiels sur les méthodes numériques
Si vous avez des questions concernant la méthode Regula Falsi (méthode des fausses positions) ou son code source dans la programmation C présentée ci-dessus, mentionnez-les dans les commentaires ci-dessous.